Modeling the COVID-19 Pandemic
Contents
Modeling the COVID-19 Pandemic¶
Reading¶
Bregman D.J., A.D. Langmuir, 1990. Farr’s law applied to AIDS projections. JAMA, 263:1522–1525. doi: 10.1001/jama.263.11.1522.
King, A.A., M.D. de Cellès, F.M.G. Magpantay, and P. Rohani, 2015. Avoidable errors in the modelling of outbreaks of emerging pathogens, with special reference to Ebola, Proc. R. Soc. B. 28220150347 http://doi.org/10.1098/rspb.2015.0347.
Murray, C.J.L., and IHME COVID-19 health service utilization forecasting team, 2020. Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator-days and deaths by US state in the next 4 months, https://www.medrxiv.org/content/10.1101/2020.03.27.20043752v1.full-text
Jewell, N.P., J.A. Lewnard, and B.L. Jewell, 2020. Predictive Mathematical Models of the COVID-19 Pandemic: Underlying Principles and Value of Projections, JAMA, 323(19):1893-1894. doi:10.1001/jama.2020.6585
Froese, H., 2020. Infectious Disease Modelling: Fit Your Model to Coronavirus Data, Towards Data Science, https://towardsdatascience.com/infectious-disease-modelling-fit-your-model-to-coronavirus-data-2568e672dbc7; https://github.com/henrifroese/infectious_disease_modelling
Smith, D., and L. Moore, 2004. The SIR model for spread of disease, Convergence, https://www.maa.org/press/periodicals/loci/joma/the-sir-model-for-spread-of-disease-introduction
Models of epidemics¶
This notebook explores two basic approaches to modeling the spread of a communicable disease through a population. There are more complicated approaches than are considered here, but these are common, and the predictions of COVID-19 infections, ICU beds, and deaths are often based on variations of these models.
SIR models¶
Mathematical models of epidemics date back to the early 1900s.
One of the simplest models of epidemics is the SIR model, which partitions the population into three disjoint groups: Susceptible, Infected, and Recovered (or Removed).
The SIR model treats the population as fixed: no births, immigration, emigration, or deaths from other causes. It ignores the possibility of carriers, population heterogeneity, or geographic heterogeneity. It treats everyone as equivalent and assumes the population “mixes” perfectly.
Here are the state variables of the SIR model:
\(N\): initial population size
\(S(t)\): number of susceptible individuals in the population at time \(t\)
\(I(t)\): number of infected individuals in the population at time \(t\)
\(R(t)\): number “removed” from risk (dead or recovered) in the population at time \(t\)
Assumptions:
Everyone is either susceptible, infected, or removed (recovered or dead). (There are more complex models with more “compartments.”)
There are no births, immigration, emigration, or deaths from other causes.
If a susceptible person is infected, that person eventually dies or recovers.
While a person is infected, the person is infectious.
There is no incubation period between being infected and being infectious.
If an infected person gets “close enough” to a susceptible person, the susceptible person becomes infected.
Every unit of time, every infected person exposes \(\beta\) people.
Every susceptible person exposed to an infected person becomes infected.
Every infected person exposes a disjoint group of people.
Every unit of time, a fraction \(\gamma\) of infected people recover or die.
People who recover or die are not infectious.
People who recover or die never become susceptible again.
Then \(S + I + R = N\) is constant, the initial population size.
The basic reproductive number is \(R_0 = \beta/\gamma\). Initially, when essentially the entire population is susceptible (the proportion who are infected or recovered is small compared to \(N\)), this is the number of people each infected person infects before recovering or dying. (Note that \(R_0\) has no connection to \(R\): the notation is unfortunate.)
Define \(s(t) \equiv S(t)/N\), \(i(t) \equiv I(t)/N\), and \(r(t) \equiv R(t)/N\). Then \(s+i+r = 1\) for all \(t\). There is an epidemic if \(s(0)\beta/\gamma > 1\): the rate at which susceptible people are getting infected is greater than the rate at which infected people are recoving.
The parameters of the model are:
\(\beta\), the number of exposed people per unit of time per infected persion
\(\gamma\), the fraction of infected people who are removed (recover or die) per unit time
The state of the population evolves according to three coupled differential equations:
\(dS/dt = -\beta I S/N\)
\(dI/dt = \beta I S/N - \gamma I\) (equivalently, \(di/dt = \beta is - \gamma i\))
\(dR/dt = \gamma I\)
Another interesting variable is the cumulative number of infections, \(C\).
\(dC/dt = \beta I S/N\); \(C(0) = I(0)\).
The SIR model has some built-in features that might not match reality. First, note that the derivative of \(R\) is always non-negative and proportional to \(I\). Since \(R \le N\) and \(N\) is finite, \(I\) must eventually be zero; that is, the SIR implies that eventually the entire population will be disease-free. Once \(I=0\), it can never grow again, since the derivative of \(I\) is proportional to \(I\). (If nobody is infected, nobody can infect anyone.) Epidemics that follow the SIR model are necessarily self-limiting.
That isn’t the case if immunity wears off over time (or if the population is not isolated). In that case, we might we parametrize the transition from recovered to susceptible by assuming that a fraction \(\delta\) of \(R\) return to \(S\) in each time period. (There are other ways we could do this, for instance, having a variable “lag” between recovery and becoming susceptible again.) That yields:
\(dS/dt = -\beta I S/N + \delta R\)
\(dI/dt = \beta I S/N - \gamma I\) (equivalently, \(di/dt = \beta is - \gamma i\))
\(dR/dt = \gamma I - \delta R\)
In this model, \(I\) does not necessarily go to zero eventually.
Other generalizations include separate “compartments” for dead versus recovered), needing an ICU bed, etc., as well as time-varying values of \(\beta\) to account for lockdowns or other policy interventions, heterogeneity in the population, and more.
Let’s run this model (in discrete time) for a population of \(N=1,000,000\) people of whom 0.05% are initially infected. We will take the time interval to be 1 day, the period of infectiousness to be \(1/\gamma = 14\) days, and \(R_0 = 2 = \beta/\gamma\), so \(\beta = 2 \gamma = 1/7\). We will start with \(\delta=0\) (no re-infections).
# boilerplate
import numpy as np
import scipy as sp
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
from ipywidgets import interact, interactive, fixed, interact_manual
import ipywidgets as widgets
from IPython.display import clear_output, display, HTML
def sir_model(N, i_0, beta=1, gamma=1, delta=0, steps=365):
'''
Run SIR model as coupled finite-difference equations.
Assumes that initially a fraction i_0 of the population of N people is infected and
everyone else is susceptible (none has died or recovered).
Parameters
-----------
N : int
population size
i_0 : double in (0, 1)
initial fraction of population infected
beta : double in [0, infty)
number of encounters each infected person has per time step
gamma : double in (0, 1)
fraction of infecteds who recover or die per time step
delta : double in (0, 1)
fraction of recovereds who become susceptible per time step
steps : int
number of steps in time to run the model
Returns
--------
S, I, R, C
S : list
time history of susceptibles
I : list
time history of infecteds
R : list
time history of recovered/dead
C : list
cumulative number of infections over time
'''
assert i_0 > 0, 'initial rate of infection is zero'
assert i_0 <= 1, 'infection rate greater than 1'
assert beta >= 0, 'beta must be nonnegative'
assert gamma > 0, 'gamma must be positive'
assert gamma < 1, 'gamma must be less than 1'
assert delta >= 0, 'delta must be nonnegative'
assert delta < 1, 'delta must be less than 1'
S = np.zeros(steps)
I = np.zeros(steps)
R = np.zeros(steps)
C = np.zeros(steps)
I[0] = int(N*i_0)
C[0] = I[0]
S[0] = N-I[0]
for i in range(steps-1):
new_i = beta*I[i]*S[i]/N
S[i+1] = max(0, S[i] - new_i + delta*R[i])
I[i+1] = max(0, I[i] + new_i - gamma*I[i])
R[i+1] = max(0, R[i] + gamma*I[i] - delta*R[i])
C[i+1] = C[i] + new_i
return S, I, R, C
def plot_sir(N, i_0, beta=2/14, gamma=1/14, delta=0, steps=365, verbose=False):
'''
Plot the time history of an SIR model.
Parameters
-----------
N : int
population size
i_0 : double in (0, 1)
infection rate at time 0
beta : double in [0, infty)
number of encounters each infected person has per time step
gamma : double in (0, 1)
fraction of infecteds who recover or die per time step
delta : double in (0, 1)
fraction of recovereds who become susceptible per time step
steps : int
number of time steps to run the model
verbose : Boolean
if True, return the model predictions
Returns (if verbose == True)
--------
S : list
susceptibles as a function of time
I : list
infecteds as a function of time
R : list
recovereds as a function of time
C : list
cumulative incidence as a function of time
'''
S, I, R, C = sir_model(N, i_0, beta=beta, gamma=gamma, delta=delta, steps=steps)
times = list(range(steps))
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.plot(times, I, linestyle='--', color='r', label='Infected')
ax.plot(times, S, linestyle='-', color='b', label='Susceptible')
ax.plot(times, R, linestyle=':', color='g', label='Recovered')
ax.plot(times, C, linestyle='-.', color='k', label='Tot infect.')
ax.legend(loc='best')
plt.show()
if verbose:
return S, I, R, C
i_0 = 0.0005
N = int(10**6)
steps = 365
plot_sir(N, i_0)
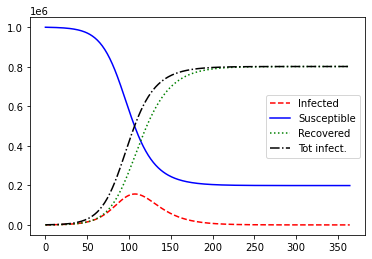
For these parameters, the number of infections is shaped like a bell curve and the cumulative number of infections is shaped like a CDF: it is “sigmoidal” (vaguely “S”-shaped). You might imagine fitting a scaled CDF to the curve. Essentially, the IHME model fits a scaled Gaussian CDF to the total number of infections. (More on this below.)
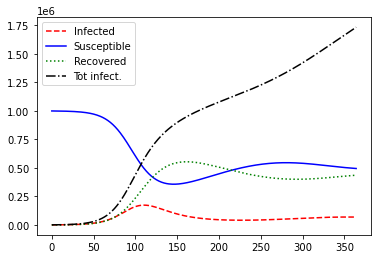
What if immunity wears off over time? Let’s try a positive value of \(\delta\):
plot_sir(N, i_0, delta=0.01)
interact(plot_sir, N=fixed(N),
i_0 = widgets.FloatSlider(min=0, max=1, value=i_0),
beta=widgets.FloatSlider(value=2/14, min=0.01, max=100),
gamma=widgets.FloatSlider(value=1/14, min=0, max=1, step=0.01),
delta=widgets.FloatSlider(value=0, min=0, max=1, step=0.01),
steps=fixed(steps),
verbose=fixed(False))
<function __main__.plot_sir(N, i_0, beta=0.14285714285714285, gamma=0.07142857142857142, delta=0, steps=365, verbose=False)>
Fitting the SIR model to data¶
Now we will use least squares to fit the SIR model to a time history of infection data collected by researchers at Johns Hopkins University. See https://github.com/CSSEGISandData
This exercise is for illustration. There are many reasons to be wary of this modeling:
There are serious issues with the data quality: these are cases that were reported according to the rules and circumstances of where they were detected. For mortality (rather than incidence), excess mortality might give a more accurate measure.
The model is a cartoon, not “physics” of epidemics, and it omits many factors that plausibly matter. It is not clear what estimates of the parameters mean when the model is wrong.
Absent a trustworthy generative model for the data, it is not clear how to assess or interpret the uncertainty of the estimates.
If the estimated model is to be used for prediction, there is no obvious way to assign meaningful uncertainties to the predictions.
The optimization problem to fit the parameters has no statistical content or motivation. It is not clear that it yields an estimate that is “good” in a useful sense.
The objective function is not convex in the model parameters, and the optimization algorithm is not guaranteed to solve the optimization problem.
The data record total “confirmed” cases as a function of time, deaths, and recoveries: \(C(t)\)
from scipy.optimize import curve_fit # nonlinear least squares
def f(x, beta, gamma):
'''
Model cumulative infections
This is just a wrapper for a call to sir_model, to generate a set of
predictions of the cumulative incidence for curve fitting
'''
return sir_model(N, i_0, beta, gamma, delta=0, steps=len(x))[3] # C
# test f
N = int(10**6)
i_0 = 0.0005
x = range(25)
y = f(x, 1/7, 1/14 )
y
array([ 500. , 571.39285714, 647.87464122, 729.80689646,
817.5766761 , 911.59831599, 1012.31532767, 1120.20241833,
1235.76764552, 1359.55471484, 1492.14542917, 1634.1622985 ,
1786.27131969, 1949.18493587, 2123.66518564, 2310.5270524 ,
2510.64202461, 2724.94187786, 2954.42268994, 3200.14910031,
3463.25882519, 3744.96743963, 4046.57343789, 4369.46358264,
4715.11855381])
# test curve_fit
popt, pvoc = curve_fit(f, x, y, p0=[1, 0.5], bounds = (0, [np.inf, 1]))
popt
array([0.14285714, 0.07142857])
# try some real data from the JHU site
import pandas as pd
# data for countries. THIS IS A "LIVE" DATASET THAT IS UPDATED FREQUENTLY
url = "https://raw.githubusercontent.com/CSSEGISandData/COVID-19/master/csse_covid_19_data/csse_covid_19_time_series/time_series_covid19_confirmed_global.csv"
df = pd.read_csv(url, sep=",")
df.head()
| Province/State | Country/Region | Lat | Long | 1/22/20 | 1/23/20 | 1/24/20 | 1/25/20 | 1/26/20 | 1/27/20 | ... | 3/4/22 | 3/5/22 | 3/6/22 | 3/7/22 | 3/8/22 | 3/9/22 | 3/10/22 | 3/11/22 | 3/12/22 | 3/13/22 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | NaN | Afghanistan | 33.93911 | 67.709953 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 174214 | 174331 | 174582 | 175000 | 175353 | 175525 | 175893 | 175974 | 176039 | 176201 |
| 1 | NaN | Albania | 41.15330 | 20.168300 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 272030 | 272030 | 272210 | 272250 | 272337 | 272412 | 272479 | 272552 | 272621 | 272663 |
| 2 | NaN | Algeria | 28.03390 | 1.659600 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 265186 | 265227 | 265265 | 265297 | 265323 | 265346 | 265366 | 265391 | 265410 | 265432 |
| 3 | NaN | Andorra | 42.50630 | 1.521800 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 38434 | 38434 | 38434 | 38620 | 38710 | 38794 | 38794 | 38794 | 38794 | 38794 |
| 4 | NaN | Angola | -11.20270 | 17.873900 | 0 | 0 | 0 | 0 | 0 | 0 | ... | 98796 | 98796 | 98806 | 98806 | 98829 | 98855 | 98855 | 98855 | 98909 | 98927 |
5 rows × 786 columns
# data for Denmark
DK = df.loc[(df["Country/Region"] == "Denmark") & df["Province/State"].isna()] # Denmark
DK = DK.drop(['Province/State','Country/Region','Lat','Long'], axis=1).T # remove fields we don't need
y = DK.to_numpy() # turn series into a vector
y = y[np.nonzero(y)] # remove the data before the first detected case
x = range(len(y)) # for model-fitting and plotting
print(len(y),y)
746 [ 1 1 3 4 4 6 10 10 23
23 35 90 262 442 615 801 827 864
914 977 1057 1151 1255 1326 1395 1450 1591
1724 1877 2046 2201 2395 2577 2860 3107 3386
3757 4077 4369 4681 5071 5402 5635 5819 5996
6174 6318 6511 6681 6879 7073 7242 7384 7515
7695 7912 8073 8210 8445 8575 8698 8851 9008
9158 9311 9407 9523 9670 9821 9938 10083 10218
10319 10429 10513 10591 10667 10713 10791 10858 10927
10968 11044 11117 11182 11230 11289 11360 11387 11428
11480 11512 11593 11633 11669 11699 11734 11771 11811
11875 11924 11948 11962 12001 12016 12035 12099 12139
12193 12217 12250 12294 12344 12391 12391 12391 12527
12561 12615 12636 12675 12675 12675 12751 12768 12794
12815 12832 12832 12832 12878 12888 12900 12916 12946
12946 12946 13037 13061 13092 13124 13173 13173 13173
13262 13302 13350 13390 13438 13438 13438 13547 13577
13634 13725 13789 13789 13789 13996 14073 14185 14306
14442 14442 14442 14815 14959 15070 15214 15379 15483
15617 15740 15855 15940 16056 16127 16239 16317 16397
16480 16537 16627 16700 16779 16891 16985 17084 17195
17374 17547 17736 17883 18113 18356 18607 18924 19216
19557 19890 20237 20571 20571 21393 21847 22436 22905
23323 23799 24357 24916 25594 26213 26637 27072 27464
27998 28396 28932 29302 29680 30057 30379 30710 31156
31638 32082 32422 32811 33101 33593 34023 34441 34941
35392 35844 36373 37003 37763 38622 39411 40356 41412
42157 43174 44034 45225 46351 47299 48241 49594 50530
51753 53180 54230 55121 55892 56958 57952 58963 60000
61078 62136 63331 64551 65808 67105 68362 69635 70485
71654 73021 74204 75395 76718 78354 79352 80481 81949
83535 85140 86743 88858 90603 92649 94799 97357 100489
103564 107116 109758 113095 116087 119779 123813 128321 131606
134434 137632 140175 143472 146341 149333 151167 153347 155826
158447 161230 163479 165930 167541 168711 170787 172779 174995
176837 178497 180240 181486 182725 183801 185159 185159 187320
188199 189088 189895 190619 191505 192265 193038 193917 194671
195296 195948 196540 197208 197664 198095 198472 198960 199357
199782 200335 200773 201186 201621 202051 202417 202887 203365
203793 204067 204362 204799 205183 205597 206065 206617 207081
207577 208027 208556 209079 209682 210212 210732 211195 211692
212224 212798 213318 213932 214326 214839 215264 215791 217798
218660 219305 219918 220459 221071 221842 222629 223415 224258
224848 225505 226777 227031 225030 225844 226633 227049 228013
228692 229902 230603 231265 231973 232718 233318 233797 234317
234931 235648 236346 237101 237792 238306 238869 239532 240330
241007 241731 242633 243374 244065 244868 245761 246463 247010
247622 248326 248950 249785 250554 250554 252045 252912 253673
254482 254482 256482 257505 258182 259056 259988 260913 262159
263514 264465 265539 266503 267339 268255 269343 270557 271908
272659 273494 274413 275207 276280 277399 278396 279434 280383
281227 282135 283089 284117 285044 285636 286489 286948 287325
288229 288704 289122 289559 289874 290111 290333 290686 291017
291220 291463 291652 291801 291956 292179 292352 292574 292769
292943 293094 293337 293677 294152 294478 294925 295317 295654
296196 296885 297543 298094 298614 299223 300071 301126 302328
303469 304429 305459 306100 306944 307764 308615 309420 310127
310876 311520 312292 312851 314135 314983 316068 316807 317700
318485 319295 320222 321154 322019 322965 323786 324721 325725
326887 327972 329010 329927 330777 331736 332622 333815 334799
335722 336746 337466 338240 339580 340567 341549 342474 343351
344088 344850 345693 346518 347212 347909 348347 348979 349440
349891 350405 350996 351553 351939 352373 352636 353061 353431
353744 354068 354393 354645 354913 355257 355603 355944 356326
356684 357037 357370 357827 358369 358796 359237 359663 360031
360411 360888 361461 362068 362738 363356 363900 364464 365051
365840 366607 367307 368060 368651 369403 370159 371286 372533
373803 375065 376414 377825 379078 380949 382796 384580 386251
387783 389240 391221 393199 395797 398048 400145 402561 404855
407417 410434 412566 417151 420099 423322 426992 430891 434798
438811 442881 446676 450091 453802 458001 462427 466817 470893
474637 478927 483253 487401 492521 497201 501760 506085 509111
516257 522581 529210 536195 542794 548400 554389 562188 570502
579275 589274 600468 609062 617274 627356 647934 661320 673807
685036 685036 685036 726071 739071 762299 783702 802397 823282
831236 840037 865110 893393 919388 937649 950237 969485 983899
1006295 1030638 1056389 1080003 1105037 1131206 1159986 1193479 1232238
1272864 1319695 1355815 1397833 1438181 1484771 1531518 1582551 1636206
1677289 1713485 1742569 1787935 1842936 1887161 1927340 1966530 2003042
2037891 2087689 2142809 2196556 2244726 2289076 2327399 2356873 2399851
2442799 2483399 2519057 2552361 2578051 2606934 2637414 2666454 2691663
2714447 2731806 2748260 2764838 2783399 2803857 2803857 2837501 2853236
2864063 2876288 2891763 2908721 2923030 2936856 2943947 2950605]
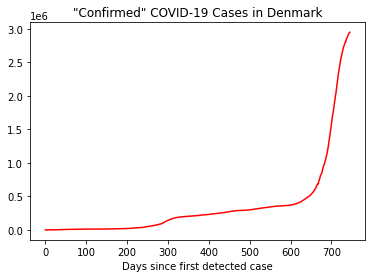
plt.plot(x,y, linestyle='-', color='r')
plt.title('"Confirmed" COVID-19 Cases in Denmark')
plt.xlabel('Days since first detected case')
Text(0.5, 0, 'Days since first detected case')
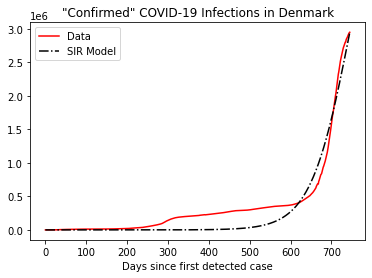
N = 5792202 # estimated population of DK in 2020
i_0 = y[0]/N # initial prevalence
x = np.array(range(len(y)))
# fit the model by nonlinear least squares
popt, pvoc = curve_fit(f, x, y, p0=[1, 0.5], bounds = (0, [500, 1]), maxfev=10000)
popt
array([2.11506788e-02, 4.12605498e-16])
S, I, R, C = sir_model(N, i_0, beta=popt[0], gamma=popt[1], delta=0, steps=len(y))
times = list(range(len(y)))
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.plot(times, y, linestyle='-', color='r', label='Data')
ax.plot(times, C, linestyle='-.', color='k', label='SIR Model')
ax.legend(loc='best')
plt.xlabel('Days since first detected case')
plt.title('"Confirmed" COVID-19 Infections in Denmark')
plt.show()
What happens if we run the model into the future?
S, I, R, C = plot_sir(N, i_0, beta=popt[0], gamma=popt[1], delta=0, steps=1000, verbose=True)
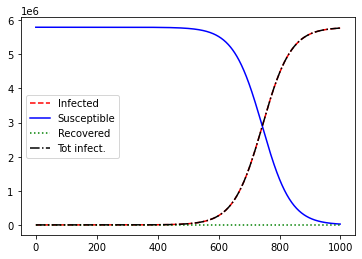
The total number of infections stabilizes, and the pandemic abates. The effective reproductive number \(R_0\) is less than 1.
Let’s do a quick sanity check. Recall that \(R_0 = \beta/\gamma\) for the SIR model initially, when the number infected, recovered, or dead are negligible compared to the total population. Once some of the population has recovered, some of the people an infectious person encounters wiil be people who have recovered and not susceptible to reinfection (according to the model). To first order, \(\beta\) is effectively reduced by \(S/N\).
# R_0 at the time the first infection is detected
popt[0]/popt[1] # greater than 1. According to the model, the infection will spread if R_0 > 1.
51261262636618.664
# After 1000 timesteps, R_0 is different
(S[-1]/N)*popt[0]/popt[1] # less than 1: According to the model, the infection will abate.
219047240451.27252
Fitting curves to the cumulative incidence function¶
The SIR model and its variants attempt to capture the dynamics of transmission and recovery, For some parameter choices, that leads to a sigmoidal shape for the cumulative incidence of infections.
Some pandemic predictions simply fit a sigmoidal function to the cumulative number of infections, an approach that dates back to William Farr in the 1800s. King et al. (2015) showed that this approach does not work well for AIDS or Ebola. Nonetheless, this is the approach the IHME takes: they fit a scaled and shifted Gaussian cdf to cumulative incidence.
Sigmoidal Models¶
Common sigmoidal models include CDFs of unimodal distributions (such as the Gaussian cdf \(\Phi(x)\)) and the sigmoid function \(1/(e^{-x} + 1)\), the inverse of the logistic function.
To allow this function to be shifted and scaled, we can introduce the family of curves
The parameter \(a\) controls where the function crosses \(c/2\); \(b\) controls how rapidly it increases, and \(c\) is its asymptotic limit.
Let’s fit this to the Danish data.
def g(x, a, b, c):
'''
Wrapper for the sigmoid to pass to the curve-fitting function
'''
return c/(np.exp(-b*(x-a))+1)
# test g visually.
z = np.array(range(-8,15,1))
plt.plot(z, g(z,3,1/2,5))
[<matplotlib.lines.Line2D at 0x7f98b0dde0a0>]
# fit the DK data
popts, pvocs = curve_fit(g, x, y, p0=[len(x)/2, 0.02, np.max(y)/2], bounds = ([0, 0, 0], [500, 500, N]), maxfev=10000)
popts
array([5.00000000e+02, 1.11921669e-02, 1.16292975e+06])
# plot
Cs = g(x, popts[0], popts[1], popts[2])
times = list(range(len(y)))
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.plot(times, y, linestyle='-', color='r', label='Data')
ax.plot(times, C[:len(times)], linestyle='-.', color='k', label='SIR Model')
ax.plot(times, Cs, linestyle=':', color='b', label='Sigmoid Model')
ax.legend(loc='best')
plt.xlabel('Days since first detected case')
plt.title('"Confirmed" COVID-19 Infections in Denmark')
plt.show()
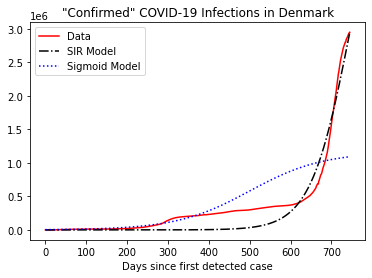
Both models agree reasonably well with past data. But they have rather different predictions about the future.
Let’s look at how the predictions vary over time, as the dataset grows.
def plot_predictions(y, n, points):
'''
plot SIR and sigmoid models fitted to the first n data
Parameters
----------
y : list of floats
number of infections at each time point
n : int
fit the models to the first n elements of y
points : int
number of time points for which to plot the prediction
Returns
-------
no return value
'''
# fit the two models
x = list(range(len(y)))
popt, pvoc = curve_fit(f, x[:n], y[:n], p0=[1, 0.5], bounds = (0, [500, 1]),
maxfev=10000)
popts, pvocs = curve_fit(g, x[:n], y[:n], p0=[len(x)/2, 0.02, np.max(y)/2],
bounds = ([0, 0, 0], [500, 500, N]), maxfev=10000)
times = list(range(points))
S, I, R, C = sir_model(N, i_0, beta=popt[0], gamma=popt[1], delta=0, steps=points)
Cs = g(times, popts[0], popts[1], popts[2])
fig, ax = plt.subplots(nrows=1, ncols=1)
ax.plot(x, y, linestyle='-', color='r', label='Data')
ax.plot(times, C, linestyle='-.', color='k', label='SIR Model')
ax.plot(times, Cs, linestyle=':', color='b', label='Sigmoid Model')
ax.vlines(x[n-1], 0, np.max([C, Cs]), label='truncation time')
ax.legend(loc='best')
plt.xlabel('Days since first detected case')
plt.title('"Confirmed" COVID-19 Infections in Denmark')
plt.show()
interact(plot_predictions, y=fixed(y),
n = widgets.IntSlider(min=20, max=len(y), value=100),
points=fixed(2*len(y)))
<function __main__.plot_predictions(y, n, points)>
The predictions depend on the model and details of the data. A few additional days of data can drastically change the predictions. For some end dates, the two models have nearly identical predictions; for others, they differ by a factor of 20 or more.
Unlike the SIR model, the sigmoid model does not “know” how many people are in the population, so even if recovery conveys immunity, the cumulative number of infections in the sigmoid model can exceed the size of the population.
This mindless “curve fitting” approach is not a reliable basis for predicting the course of the pandemic, predicting ICU demand, predicting the effect of an intervention, allocating resources, or setting public policy. It is a mechanical application of models and algorithms to data, not science.
Unsurprisingly, models of this type do not predict infections well in practice. The most-cited predictions have been those promulgated by the Institute for Health Metrics and Evaluation (IHME) at the University of Washington. They say,
Our model is designed to be a planning tool for government officials who need to know how different policy decisions can radically alter the trajectory of COVID-19 for better or worse.
Our model aimed at helping hospital administrators and government officials understand when demand on health system resources will be greatest. (http://www.healthdata.org/covid/faqs#differences%20in%20modeling, last visited 23 January 2021)
IHME’s model is described here. Early in the pandemic, IHME predicted that there would be about 60,000 COVID-19 deaths in ths U.S. As of 18 February 2021, there have been more than 490,000. Between March and August, 2020, next-day deaths were within the IHME 95% prediction interval only about 30% of the time, despite revisions of the model https://arxiv.org/abs/2004.04734. (We shall not delve into how IHME produces its prediction intervals.) See also https://www.vox.com/future-perfect/2020/5/2/21241261/coronavirus-modeling-us-deaths-ihme-pandemic.
One feature of the sigmoidal models is that they predict rapid declines after the peak (the decline is just as rapid as the rise), a feature that some politicians like. That feature is built into the sigmoidal curve: it is an assumption, not something that comes from the data.
There are also more complicated models of pandemics, including models with more “compartments,” models based on other sigmoidal functions (such as the Gaussian CDF), and models that allow various kinds of heterogeneity within the population and simulate interactions between individuals. Some have proved more accurate than others. Just how poorly some models perform is obscured by the practice of revising the model and projections frequently–even daily.
Sometimes, a moddle with little substantive foundation can nonetheless predict the behavior of a system, at least if the system is not changing quickly. Accurate predictions of the effect of interventions (masks, lockdowns, vaccination, and so on) require a close tie between the world and the model: the model needs a substantive basis. For causal inferences, the model needs to be a generative model or response schedule.
George Box famously wrote, “all models are wrong, but some are useful.” While that quotation is often invoked as a general license to throw models at data, it should instead prompt questions:
useful for what?
how can you tell whether a model is useful for a particular goal?
In the same paper, Box wrote, “It is inappropriate to be concerned with mice when there are tigers abroad.” Most of the fretting people do about statistical models is at the level of mice (e.g., asymptotics under unrealistic assumptions), while the problems with most statistical models are tigers: the models have little or no connection to the actual scientific question.
New variants¶
As of this writing (10 February 2021), new strains of COVID-19 have been detected in the UK, South Africa, and the US, where cases of the new strain have a doubling time of about 10 days. The UK strain is estimated to be 50% to 70% more transmissible than the original virus. There is mounting evidence that the strain is also more lethal. https://www.wsj.com/articles/new-u-k-covid-19-variant-could-be-more-deadly-british-officials-say-11611338370 (last visited 22 January 2021).

